Thanks Michael,
Very interesting page! But it seems to
contradict your statement where it says:
It is known no
non-constant
polynomial
function P(n) with integer coefficients exists that
evaluates to a prime number for all integers n. The proof is: Suppose such a polynomial
existed. Then P(1) would evaluate
to a prime p, so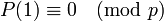 
. But for any k, 
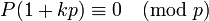also, so P(1 + kp) = p (as it is prime and divisible by p),
but the only way P(1 + kp) = P(1) for all k is if the
polynomial function is constant.
If I had been a mathematician instead of an engineer,
I might have known that for presenting earlier. Your suggested set of
functions are no “non-constant
polynomials” if they iterate the primes. Whatever that “non-constant polynomials” means!
Again, the precision of my original statement could have been greatly improved,
and thanks for your addition to the precise constraints on the which no functions exist might be useful
for other mathemticians to read, if interested.
End of soap box.
Sincerely,
Rich Cooper
EnglishLogicKernel.com
Rich AT EnglishLogicKernel DOT com
9 4 9 \ 5 2 5 - 5 7 1 2
From: ontolog-forum-bounces@xxxxxxxxxxxxxxxx
[mailto:ontolog-forum-bounces@xxxxxxxxxxxxxxxx] On Behalf Of Michael Gruninger
Sent: Thursday, October 14, 2010
11:36 AM
To: ontolog-forum@xxxxxxxxxxxxxxxx
Subject: Re: [ontolog-forum] HOL
decidability [Was: using SKOS forcontrolled values for controlledvocabulary]
On 10-10-14 1:15 PM, Rich Cooper wrote:
Hi Doug,
Thanks for you post, you seem to be honestly trying to
understand what I meant by the statement "there is no function that can
iterate the primes", and perhaps I should have originally said
"directly, without iterating other types", which seems to have set
off this mess. But I expected Menzel to make an honest answer instead of
an ad hominem attack.
The point is that there is no function which takes
primes as its domain and ranges over the primes.
Actually, there is indeed such a function.
Matiyasevich's
theorem says:
Every recursively
enumerable set is Diophantine,
that is, every recursively enumerable set is
equivalent to the integer solutions of some polynomial.
Since the set of prime numbers is recursively enumerable, there exists a
polynomial function
whose integer solutions are exactly the prime numbers.
You might even check out the page
http://en.wikipedia.org/wiki/Prime_number_formulas
for examples of such functions.
As a wise person said earlier in this thread
"we've made progress if you get off the soap box. "
- michael