Thanks for the reply and the challenging discussion here.
I want to try defending a "holistic and integral" point of view -- that is concerned with very broad issues, and attempts to develop a perspective that does embrace the entire range of human thinking.
A common theme on this mailing list is a concern with "the machine interpretation of natural language" -- and if I understand this correctly, the general assumptions involve building interpretations based on the "empirical" experience of language. This approach tends to be based on a huge library of empirically-derived "context" (millions of examples).
This is an instructive subject for me -- but my main concern is the "the human interpretation of natural language" -- and the weaknesses that emerge in human communication because of misinterpretation. My interest is more in interpreting "the intended meaning" of a statement than a statistical interpretation that has no way of inferring or considering intention. This intentional (or stipulative) approach presumes that the speaker knows what he/she intends by the words they use -- and that their meaning, if confusing to the listener, can be clarified by dialogue and questions.
Is it naïve of me to even consider that it might be possible to ground "natural language" in some fundamental universal foundation? That case would not be hard to make. The answer for many people here might clearly be "yes" -- "get over it, mister, this can't happen -- or at least, never has -- and for a lot of good reasons". That is a sensible perspective.
But I am still compelled from a larger perspective to push some of these ideas -- though it is true they are hard to prove.
*
John:
Debates about how to define the word 'axiom' are as pointless as trying to define the word 'primitive'.
That's a related question that raises its ugly head from time to time.
Bruce:
One point of my message was to suggest that the concept of "axiom" seems inherently flawed or vulnerable, since in most or all cases, its authority tends to be grounded in social contract and empirical experience (we've seen a million examples and these examples "prove" our thesis by induction) rather than a strict logic method. This seems clearly true in the case of very broad/abstract "axioms" stated in words -- like those suggested by Richard -- and is apparently also true for very precise mathematical axioms stated in symbols. So, in general, I would like to move away from the concept of axiom (whatever it means) as a foundation for human thinking -- and towards some more fundamental and basic principle -- from which "all axioms could be constructed". Even axioms -- and indeed, most "primitives" as I most often encounter them -- do not seem to me to be "fundamental and primary objects". What I generally see when I look up the concept of "primitive" -- is some alphabet of composite/aggregate items that some researcher thinks can build everything. For me, this composite approach is inadequate
Like (apparently) a few others around here -- I am interested in the concept of "primitive". For me, it's a little like the chemist's interest in atomic structure. If we are looking for the absolute ground of concept formation -- "where do words come from?" -- "how are concepts defined?" -- "how are distinctions made and assigned labels?" -- somebody with my analytic instincts wants to "build" answers to those questions based on something primary. Maybe it's like creating a computer language -- where we might say -- start with “on/off” at the absolute primary level, aggregate some of those on/off elements into "bytes" or other composite units, and then define an alphabet, and then start building words that label things that seem interesting. In this sense -- the "on/off" property of some "unit" at the bottom of our construction is "the absolute foundation" for the vast edifice of the digital world.
Is there an analogy here with "the real number line"?
Maybe this is a clunky and simple-minded distinction -- but for me, it is intuitive and integral, and seems profoundly simple -- an attribute I am (perhaps naively) inclined to trust. We have a simple digital parsing that descends across levels, and keeps getting smaller until "it converges into the infinitesimal". Maybe this is indeed 19th-century mathematics -- and maybe not even that -- but for me, it looks like a basic building block for constructing a model of all human cognition and all language and all disciplines, held in one framework.
For me -- the "fundamental primitive" is something like "a distinction" -- the act of "telling two things apart" -- of saying one number is bigger than the other -- that an integral unit -- maybe some level of decimal place in an approach to the real number line can be parsed by noting some difference between formerly identical and indistinguishable elements "within that unit" -- which prior to this distinction were impossible to see and presumed not to exist.
It can be argued that all human categorization is ultimately grounded in "similarities and differences" defined more or less in exactly these terms (this is essentially the Aristotelian method of genus and species). If we can show precise algebraic representations of this process -- we might be able to "construct" absolutely any category -- as a composite/aggregate structure composed entirely of "distinctions with labels". This process of distinction that enables humans to distinguish similarities and differences is, for me, the fundamental "primitive" out of which the world of concepts -- hence of perception and ideas – is constructed. In simplest essence, “an abstraction is an aggregate of distinctions”. The task is to show how this is true.
Are distinctions related to the "cut" concept introduced by Dedekind? I tend to think so. So, for me -- the principle or concept of "cut" – where a “cut” is that "something" that appears "in between two elements that were formally one or indistinguishable" -- is the fundamental principle from which perception and understanding are constructed. Drive that analytic process to its limit -- which I suppose is continuity -- and you begin to establish what is really "primitive" -- and on the basis of which all other "higher" (composite/aggregate) elements can be constructed -- perhaps in an exact analogy with the construction of the digital world in terms of bits.
*
John:
One of the best features of the methodology established by Aristotle and his followers was to associate a question with each category of the ontology. For example, see slides 5, 6, 7 of http://www.jfsowa.com/talks/aristo.pdf I believe that developing a methodology with a question tied to each category would be more useful than debating the meaning of 'axiom'.
Bruce:
I actually spent a long time last summer staring at those slides, making interpretations of them, etc. I have been highly influenced by "integral diagrams", perhaps initially visualized through holistic intuition and then formalized. You have done very broadly inclusive work in drawing together the conceptual and philosophic foundations of ontology, and your approach has not been weighted or slanted towards an empirical approach. You give equal weight to both the broadly intuitive and universal and the precisely analytical or local, and you do it in accessible ways. For me, that is very helpful.
John:
I like the idea of using graphic conventions for illustrating the underlying structures of an ontology. The tree diagrams we use in ontology today were invented by Porphyry (or more likely by somebody even earlier) in the 3rd c. AD.
See slide 3 and 4 of aristo.pdf for the "pincushion diagrams" that Paul Slade used to illustrate the difference between Plato and Aristotle. Slide 9 for the tree of Porphyry. Slide 27 shows the rotating circles by Raymond Lull. Slides 31 to 32 for Venn diagrams.
I believe that a good methodology based on criteria such as Quine's and questions such as Aristotle's supplemented with diagrams of various kinds -- pincushions, trees, rotating circles, Ed L's examples, etc. -- can be very helpful.
I like the multiple kinds of UML diagrams, and my only complaint would be that the number of different kinds of diagrams should be open ended.
Note the diagrams in organic chemistry, Feynman diagrams in nuclear physics, circuit diagrams in EE, etc. Every subject can benefit from diagrams that are well matched to the structures it studies.
Bruce:
Thanks. All of that is great and very helpful -- though from my rather determined integral point of view -- I do tend to resist the idea that "many scattered examples help us see better".
If those examples don't fit together into a single integral/composite scheme -- as we might perhaps justify on the grounds that "we are modeling many different things, and we need different models for different things" -- I myself would start to get skeptical. I would be inclined to say -- "You have offered us an example that is helpful in an isolated context -- but it might be minimally useful if the effort involves developing a broadly inclusive general-purpose model. Your idea is a heuristic fragment -- illuminating and helpful in its particular local context, but confusing and obscuring in a larger global/integral context. If there is no other way to represent your idea, we may need to accept it in its present format, and no doubt it is useful in that form. But seen from a larger point of view, if it is possible, it would be helpful and very desirable to "translate" the particulars of your example into a broadly inclusive and universal language that fits into a larger scheme."
**
I enclose below a diagram that begins to outline a general framework I find fascinating, and which I would say is very consistent with many of the diagrams you have created or cited, John. It is similar in many ways, for example, to the "wheels" of Ramon Lull. Perhaps the taxonomic levels are similar or equivalent to the levels in the Tree of Porphyry. But I am less comfortable with the Tree of Aristotelian categories from Brentano -- which places (for example) the attributes "quantitative" and "qualitative" as twin nodes at the bottom of the cascade -- an approach I find confusing. I prefer the approach of Stanley Smith Stevens in his "levels of measurement", which defines a linear cascade of variable types that descend from broadly abstract (qualitative) to measureable (quantitative). His cascade of levels can be directly mapped into this taxonomic framework.
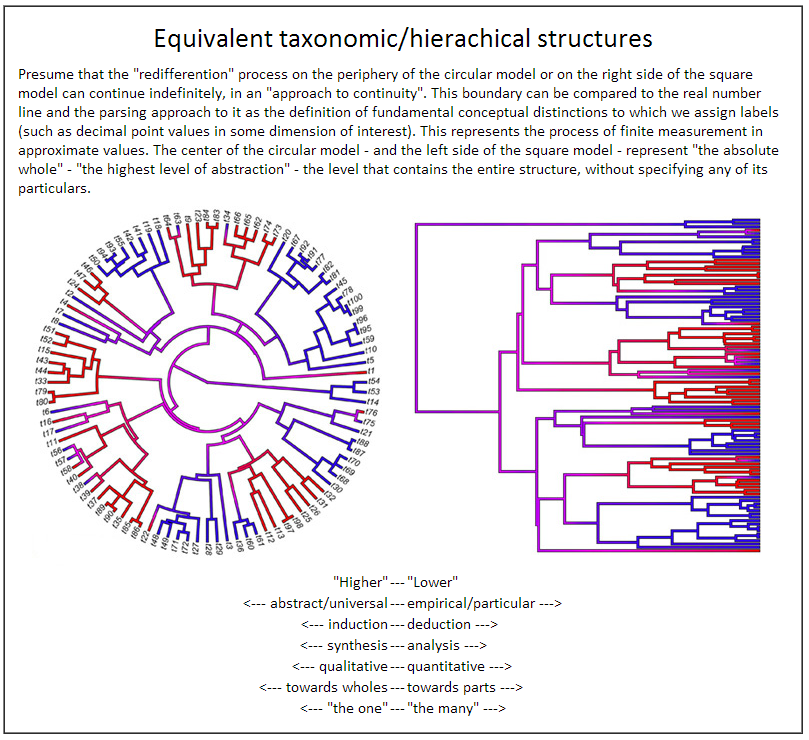
-----Original Message-----
From: ontolog-forum-bounces@xxxxxxxxxxxxxxxx [mailto:ontolog-forum-bounces@xxxxxxxxxxxxxxxx] On Behalf Of John F Sowa
Sent: Tuesday, April 22, 2014 8:31 PM
To: ontolog-forum@xxxxxxxxxxxxxxxx
Subject: Re: [ontolog-forum] axiom
Bruce, Ed B, Leo, Ed L,
Bruce
> maybe this concept of “axiom” needs a hard-edged definition in this
> “ontolog” context.
No. That wouldn't help. Debates about how to define the word 'axiom'
are as pointless as trying to define the word 'primitive'. That's a related question that raises its ugly head from time to time.
Ed B
> It is worthy of note that 99% of all ontologies, information models
> and UML models consist of nothing but terms and axioms. Everything
> captured in the model is offered without any evidence for its validity.
This point is significant. A very precise formal statement is necessary for detailed reasoning (or for designing a database or program). But if that statement comes out of thin air, its precision does not mean that it's an accurate reflection of anything in the subject matter.
Leo
> Quine’s notions on ontological commitment (e.g., his slogan, "To be is
> to be the value of a variable"), which is still an often discussed
> topic, especially in metaphysics/ontology.
That's an example of a criterion that can be used to check what the terms in an ontology refer to. Whenever you have a variable x in an ontology, you can ask the question: "What does x refer to?"
If you can't give a clear answer to that question, there is a serious problem with the ontology. One of the best features of the methodology established by Aristotle and his followers was to associate a question with each category of the ontology. For example, see slides 5, 6, 7 of http://www.jfsowa.com/talks/aristo.pdf
I believe that developing a methodology with a question tied to each category would be more useful than debating the meaning of 'axiom'.
Ed L
> the structures you arrive at may look like these...
I like the idea of using graphic conventions for illustrating the underlying structures of an ontology. The tree diagrams we use in ontology today were invented by Porphyry (or more likely by somebody even earlier) in the 3rd c. AD.
See slide 3 and 4 of aristo.pdf for the "pincushion diagrams" that Paul Slade used to illustrate the difference between Plato and Aristotle. Slide 9 for the tree of Porphyry. Slide 27 shows the rotating circles by Raymond Lull. Slides 31 to 32 for Venn diagrams.
I believe that a good methodology based on criteria such as Quine's and questions such as Aristotle's supplemented with diagrams of various kinds -- pincushions, trees, rotating circles, Ed L's examples, etc.
-- can be very helpful.
I like the multiple kinds of UML diagrams, and my only complaint would be that the number of different kinds of diagrams should be open ended.
Note the diagrams in organic chemistry, Feynman diagrams in nuclear physics, circuit diagrams in EE, etc. Every subject can benefit from diagrams that are well matched to the structures it studies.
John
_________________________________________________________________
Message Archives: http://ontolog.cim3.net/forum/ontolog-forum/
Config Subscr: http://ontolog.cim3.net/mailman/listinfo/ontolog-forum/
Unsubscribe: mailto:ontolog-forum-leave@xxxxxxxxxxxxxxxx
Shared Files: http://ontolog.cim3.net/file/ Community Wiki: http://ontolog.cim3.net/wiki/ To join: http://ontolog.cim3.net/cgi-bin/wiki.pl?WikiHomePage#nid1J
