DW> For a constraint to be expressed in Boolean logic, aren't you then moving out of the realm of propositional logic and into the realm of first order predicate logic?
RC>Yes, and with FOL come variables, algebra, and lots of good stuff. That is why it’s such a good representation if it’s available – it doesn’t bias against ANY concept representation method.
DW> Even if you only use equality (=), and non-equality ('=)
to express your constraints, don't those two act as predicates?
RC> Yes, they do. In fact any logical constraint can be expressed over a given collection of variables can be expressed algebraically, solved algebraically, and the solution implemented in the target computer.
DW> Ordinarily, I would assume that the constraints of greater than
and less then (and their cousins such as "greater than or equal to")
are part of what is included with constraint solving, at least for
numeric values, is this consistent with inferencing, or is it just a
subset of inferencing?
RC> Inferencing is a specific use of constraint propagation; if all constraints are expressed as math functions of parametric variables and constants, and when evaluated return true, then the constraint system has been solved.
David Whitten
713-870-3834
Figure 11B of my US Patent 7,209,923 is shown below:
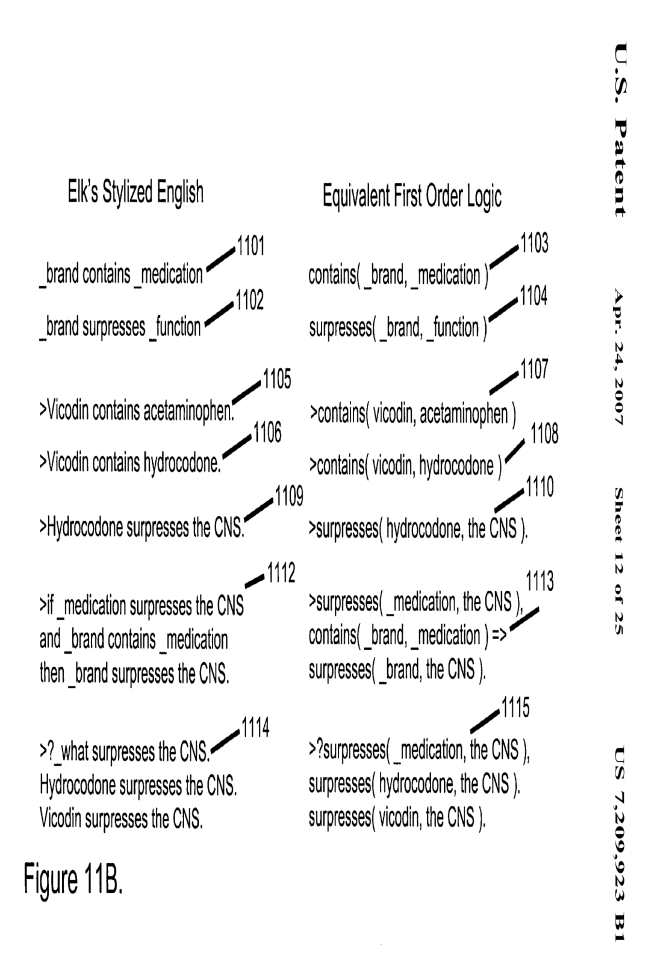
The chart shows how the English like statements on the left are interpreted in the And/Or search tree I use to resolve FOL representations. It doesn’t show some of the more subtle things it can do, such as solving equations. I had another use of that same ELK kernel that used algebraic constraint propagation, such as:
If _distance = _rate * _duration
then DRT( _distance, _rate, _duration ).
? DRT( _HowFar, 55.0, 2.0 ).
DRT( 110.0, 55.0, 2.0 ).
Or
? DRT( 110.0, _HowFast, 2.0).
DRT( 110.0, 55.0, 2.0 ).
And so on. Any equation with only one unknown can be solved by constraint propagation over an And/Or graph, resulting in an And/Or search tree.
Nodes in the search tree are instances of the same-named nodes in the graph, so various recursive visiting methods can be used to track the variables, their bindings ultimately to constants or to the “unknown” state, which is marked on the instance nodes referring to it.
-Rich
Sincerely,
Rich Cooper
EnglishLogicKernel.com
Rich AT EnglishLogicKernel DOT com
9 4 9 \ 5 2 5 - 5 7 1 2
-----Original Message-----
From: ontolog-forum-bounces@xxxxxxxxxxxxxxxx [mailto:ontolog-forum-bounces@xxxxxxxxxxxxxxxx] On Behalf Of David Whitten
Sent: Friday, October 10, 2014 10:32 AM
To: [ontolog-forum]
Subject: Re: [ontolog-forum] Constraint Solving versus Inferencing
For a constraint to be expressed in boolean logic, aren't you then
moving out of the realm of propositional logic and into the realm
of first order predicate logic?
Even if you only use equality (=), and non-equality ('=)
to express your contraints, don't those two act as predicates?
Ordinarily, I would assume that the constraints of greater than
and less then (and their cousins such as "greater than or equal to")
are part of what is included with constraint solving, at least for
numeric values, is this consistent with inferencing, or is it just a
subset of inferencing?
David Whitten
713-870-3834
On Fri, Oct 10, 2014 at 1:07 PM, Rich Cooper
<rich@xxxxxxxxxxxxxxxxxxxxxx> wrote:
> There was an article in Artificial Intelligence called “Constraint
> Propagation”, which is, IMHO, the most useful form of constraint solver. I
> don’t remember the month or year of that issue. Does anyone else remember
> that?
>
>
>
> If you google “constraint propagation algorithm”, there are several pages of
> tutorial and scholarly links that sound worth pursuing if you are just
> learning about the topic. I find constraint propagation intensely useful in
> solving day-to-day problems; it’s a way of thinking that helps order your
> thoughts. It also expresses your solutions to problems much more elegantly,
> and therefore more understandably.
>
>
>
> But note that a constraint solver need not be “iterative” in the sense of
> improving estimates step-by-step till they converge. Constraints can be
> expressed in simple Boolean logic, or in full blown first order logic. It’s
> the way you trade off one constraint for another that improves the global
> system of constraints, but there is often a true minimal cost or maximal
> gain solution to systems of constraints. It is well worth reading about.
>
>
>
> -Rich
>
>
>
> Sincerely,
>
> Rich Cooper
>
> EnglishLogicKernel.com
>
> Rich AT EnglishLogicKernel DOT com
>
> 9 4 9 \ 5 2 5 - 5 7 1 2
>
> From: ontolog-forum-bounces@xxxxxxxxxxxxxxxx
> [mailto:ontolog-forum-bounces@xxxxxxxxxxxxxxxx] On Behalf Of Simon Spero
> Sent: Friday, October 10, 2014 9:41 AM
> To: [ontolog-forum]
> Subject: Re: [ontolog-forum] Constraint Solving versus Inferencing
>
>
>
> See eg http://en.m.wikipedia.org/wiki/Constraint_logic_programming
>
> On Oct 10, 2014 11:16 AM, "David Whitten" <whitten@xxxxxxxxxx> wrote:
>
> Since we have such a large group of mathematically sophisticated people on
> this mailing list, I'd like to open a topic I know little about.
>
> I recently learned there is a Constraint Solver based on this paper
>
> http://constraints.cs.washington.edu/solvers/cassowary-tochi.pdf
>
> Described as software here:
>
> https://www.npmjs.org/package/cassowary
>
> with the implementation at the github address:
>
> https://github.com/slightlyoff/cassowary-js-refactor
>
> From their description:
>
> Constraint solvers are iterative algorithms that work towards ever more
> ideal solutions, often using some variant of Dantzig's simplex method. They
> are primarily of interest in situations where it's possible to easily set up
> a set of rules which you would like a solution to adhere to, but when it is
> very difficult to consider all of the possible solutions yourself.
>
> One of the things Inference Engines allow as the internal software of an
> expert system is to calculate the logical closure (those facts which can be
> inferred from an axiom set and a set of rules).
>
> Are these two approaches compatible?
>
>
>
> Is the Simplex method only useful for operational research, or is it useful
> in logical operations on ontologies ?
>
>
>
> Best
>
>
>
> David Whitten
>
> 713-870-3834
>
>
>
> _________________________________________________________________
> Message Archives: http://ontolog.cim3.net/forum/ontolog-forum/
> Config Subscr: http://ontolog.cim3.net/mailman/listinfo/ontolog-forum/
> Unsubscribe: mailto:ontolog-forum-leave@xxxxxxxxxxxxxxxx
> Shared Files: http://ontolog.cim3.net/file/
> Community Wiki: http://ontolog.cim3.net/wiki/
> To join: http://ontolog.cim3.net/cgi-bin/wiki.pl?WikiHomePage#nid1J
>
>
>
>
> _________________________________________________________________
> Message Archives: http://ontolog.cim3.net/forum/ontolog-forum/
> Config Subscr: http://ontolog.cim3.net/mailman/listinfo/ontolog-forum/
> Unsubscribe: mailto:ontolog-forum-leave@xxxxxxxxxxxxxxxx
> Shared Files: http://ontolog.cim3.net/file/
> Community Wiki: http://ontolog.cim3.net/wiki/
> To join: http://ontolog.cim3.net/cgi-bin/wiki.pl?WikiHomePage#nid1J
>
_________________________________________________________________
Message Archives: http://ontolog.cim3.net/forum/ontolog-forum/
Config Subscr: http://ontolog.cim3.net/mailman/listinfo/ontolog-forum/
Unsubscribe: mailto:ontolog-forum-leave@xxxxxxxxxxxxxxxx
Shared Files: http://ontolog.cim3.net/file/
Community Wiki: http://ontolog.cim3.net/wiki/
To join: http://ontolog.cim3.net/cgi-bin/wiki.pl?WikiHomePage#nid1J
